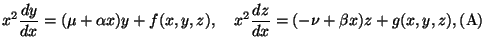
Masahiro Iwano (Chuo University)
Introduction In a previous paper (M. Iwano [8]), the author studies a nonlinear 2-system of the form
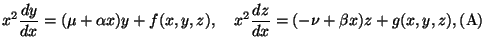
(i) ![]() and
and ![]() are commensurable positive numbers.
are commensurable positive numbers.
(ii) ![]() and
and ![]() are real constants such that
are real constants such that
![]()
(iii)
![]() and
and
![]() are holomorphic and bounded
functions of
are holomorphic and bounded
functions of ![]() for
for
![]() and their Taylor series expansions in
and their Taylor series expansions in ![]() involve neither the independent
terms nor the linear terms with respect to
involve neither the independent
terms nor the linear terms with respect to ![]() and
and ![]() :
:
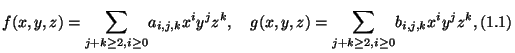
To simplify the description, we assume that

By assuming that
(iv) the sum ![]() of the quantities
of the quantities ![]() and
and ![]() is a nonzero quantity :
is a nonzero quantity :
Theorem A Apply successively two formal transformations
![]() and
and
![]() of the types :
of the types :
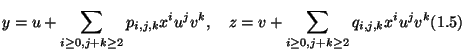
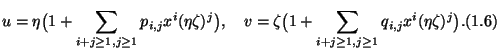
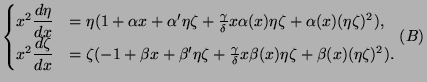
But, unfortunately, we cannot given any analytical meaning to the
power series ![]() and
and ![]() by a natural manner (which
means that they are solutions of algebraic equations or solutions of
simple differential equations.)
So, by means of Borel-Ritt Theorem, we define the
by a natural manner (which
means that they are solutions of algebraic equations or solutions of
simple differential equations.)
So, by means of Borel-Ritt Theorem, we define the ![]() and
and ![]() as holomorphic functions such that they are holomorphic and bounded in
as holomorphic functions such that they are holomorphic and bounded in ![]() for a domain of the form
for a domain of the form
The purpose of the present paper is to discuss analytical meaning of the formal transformation
![]() of the following form,
which are obtained by the composite of (1.5) and (1.6):
of the following form,
which are obtained by the composite of (1.5) and (1.6):
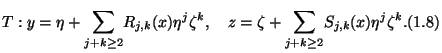
Theorem
B![]() Assume
Assume
![]() . There
is a transformation
. There
is a transformation
![]()
(i) ![]() and
and ![]() are expressed by
are expressed by
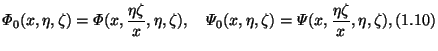
(ii) The
![]() and
and
![]() admit uniformly convergent expansions in powers of
admit uniformly convergent expansions in powers of ![]() and
and ![]() in domain (1.11) with coefficients holomorphic and
bounded in
in domain (1.11) with coefficients holomorphic and
bounded in ![]() for
for
Theorem
B![]() Assume
Assume
![]() . There
is a transformation
. There
is a transformation
![]() of the
form (1.9) which changes equations (A) to equations (B) with the
properties that:
of the
form (1.9) which changes equations (A) to equations (B) with the
properties that:
(i)
![]() and
and
![]() are expressed by
are expressed by
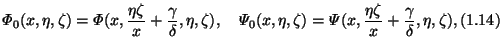
(ii) The
![]() and
and
![]() admit uniformly convergent expansions in powers of
admit uniformly convergent expansions in powers of ![]() and
and ![]() in domain (1.11) with coefficients holomorphic and
bounded in
in domain (1.11) with coefficients holomorphic and
bounded in ![]() for domain (1.12).
The coefficients are expanded to convergent power series
in
for domain (1.12).
The coefficients are expanded to convergent power series
in ![]() uniformly valid in domain (1.12), with coefficients which
are functions holomorphic and bounded in
uniformly valid in domain (1.12), with coefficients which
are functions holomorphic and bounded in ![]() for domain (1.13)
and admitting asymptotic expansions to powers in
for domain (1.13)
and admitting asymptotic expansions to powers in ![]() as
as ![]() tends to the origin through (1.13).
tends to the origin through (1.13).
Theorem
B![]() Assume
Assume
![]() . Let
. Let
![]() and
and ![]() be any angles such that
be any angles such that
(i)
![]() and
and
![]() are
expressible by(1.10), where the
are
expressible by(1.10), where the
![]() and
and
![]() are holomorphic and bounded functions in
are holomorphic and bounded functions in
![]() in a domain of the form
in a domain of the form
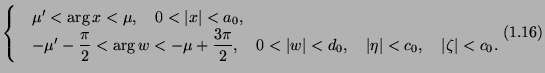
(ii) The
![]() and
and
![]() admit uniformly convergent expansions in powers of
admit uniformly convergent expansions in powers of ![]() and
and ![]() in doman (1.16), with coefficients holomorphic and bounded in
in doman (1.16), with coefficients holomorphic and bounded in ![]() for
for

The relations between the functions
![]() and
formal power series (T) will be clarified in Theorem 5.
B
and
formal power series (T) will be clarified in Theorem 5.
B![]() and Theorem 5.
B
and Theorem 5.
B![]() in
in ![]() 8, and in Theorem 5.
B
8, and in Theorem 5.
B![]() in
in ![]() 9.
9.
Remark. By the substitutions :
![]() in Theorem
in Theorem ![]() , a similar theorem holds.
, a similar theorem holds.