2012-06-20-c1-9-1.png

2012-06-20-c1-9-2.png

2012-06-20-c1-9-3.png

2012-06-20-c1-9-4.png

2012-06-20-c1-9-5.png

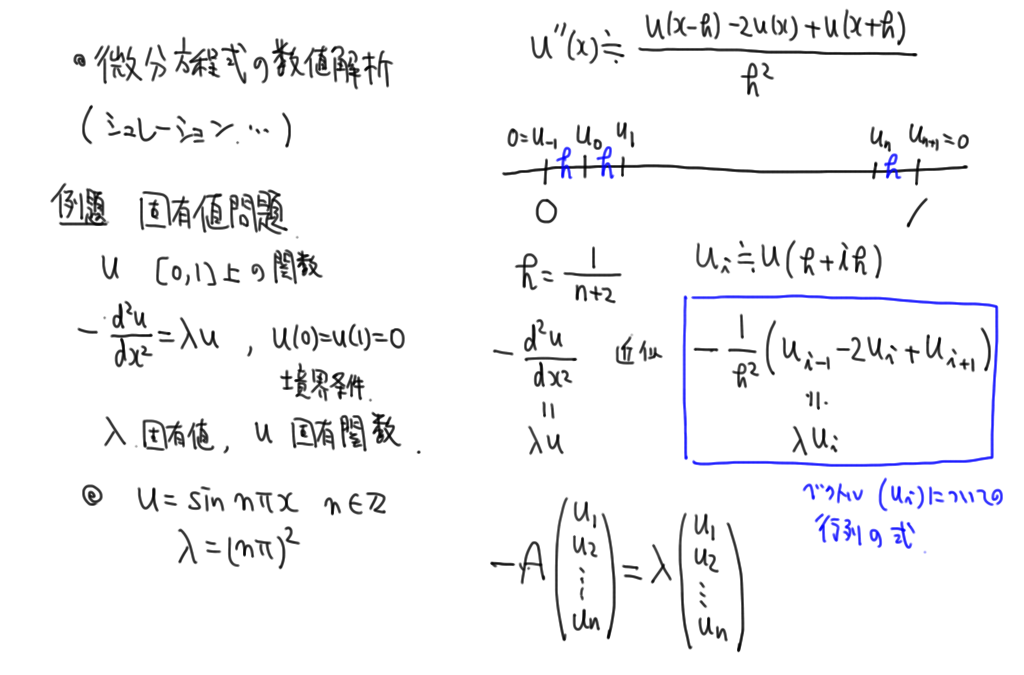
/*  -(dx^2)u = e u , u(0)=u(1)=0
   sin(x*pi)'' = - pi^2 sin(x*pi)
 */

N = 4; 
H = 1/(N+2);
A = newmat(N+1,N+1);
A[0][0] = -2; A[0][1]=1;
A[N][N-1] =1; A[N][N]=-2;
for (I=1; I< N; I++) {
  A[I][I-1] = 1; A[I][I] = -2; A[I][I+1]=1;
}
A =-A/(H*H);
F=det(t*matrix_identity_matrix(N+1)-A)$
E=pari(roots,F);
[deval(E[0]^(1/2)),deval(E[1]^(1/2)/2)];

end$

-------------------------------------------------

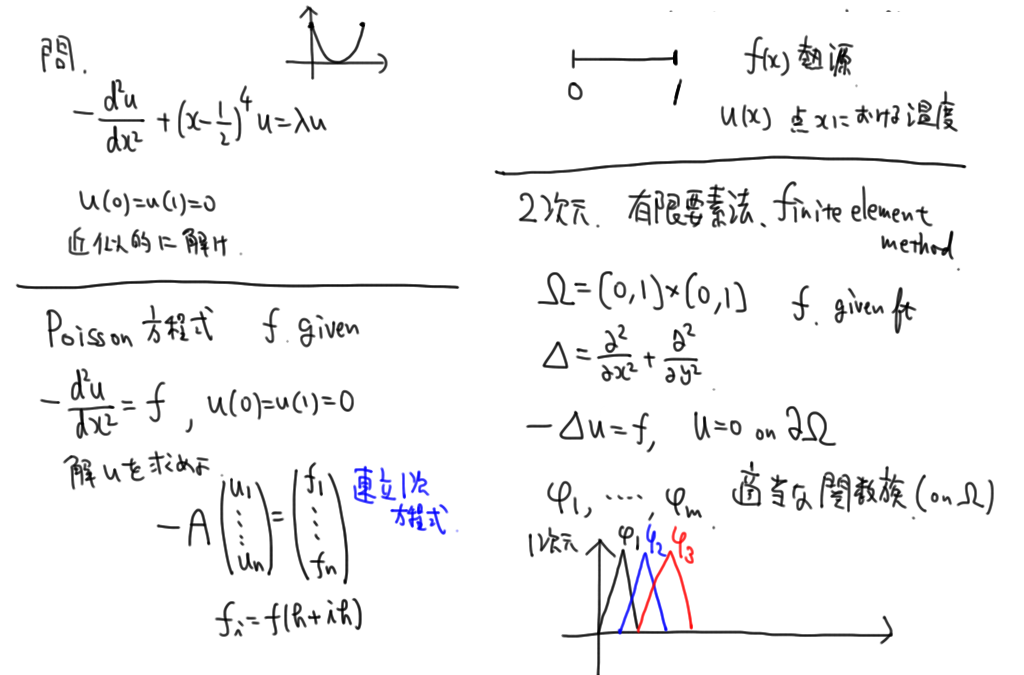
/* Solve -(dx^2)u = f , u(0)=u(1)=0
   f = sin(pi*x)
*/
N = 4; 
H = 1/(N+2);
A = newmat(N+1,N+1);
A[0][0] = -2; A[0][1]=1;
A[N][N-1] =1; A[N][N]=-2;
for (I=1; I< N; I++) {
  A[I][I-1] = 1; A[I][I] = -2; A[I][I+1]=1;
}
A =-A/(H*H);

X = newvect(N+1); 
B = newvect(N+1); 
for (I=0; I< N+1; I++) {
  X[I]=util_v(x,[I]);  
  B[I]=number_float_to_rational(deval(sin(@pi*H*(I+1))));
}
F=matrix_solve_linear(A,vtol(X),B);
Glib_math_coordinate=1;
glib_window(0,-0.1,1,0.2); glib_clear();
glib_line(0,0,1,0 | color=0xff0000);
for (I=0; I< N; I++) glib_line((I+1)*H,F[I][1],(I+2)*H,F[I+1][1]);
glib_flush();
end$

------------------------------------------------------
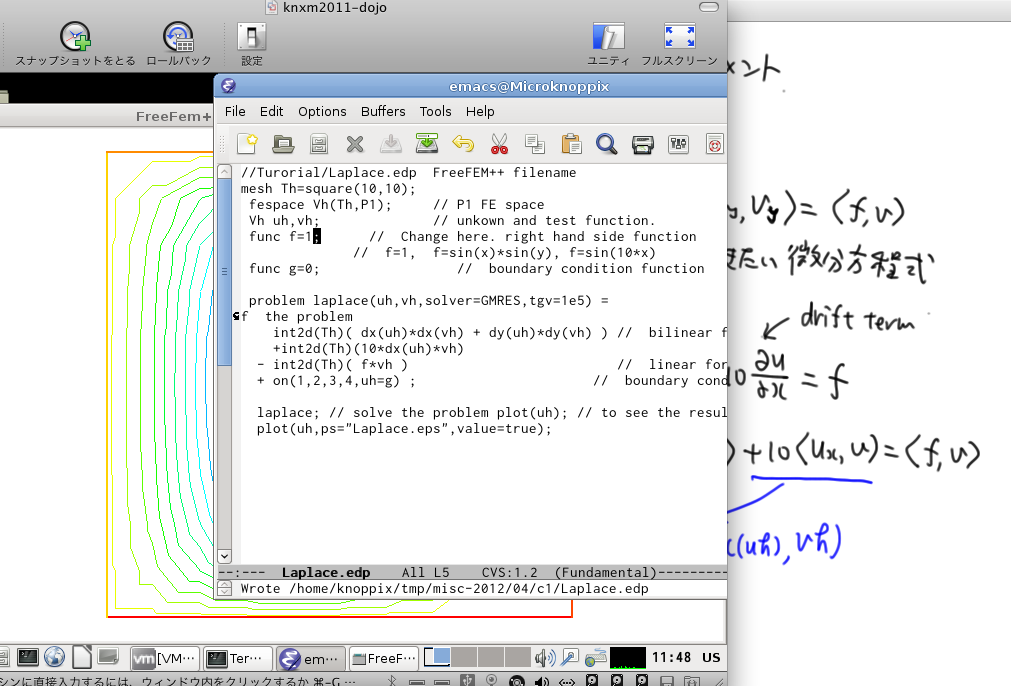
//Turorial/Laplace.edp  FreeFEM++ filename 
mesh Th=square(10,10);
 fespace Vh(Th,P1);     // P1 FE space
 Vh uh,vh;              // unkown and test function. 
 func f=1;      //  Change here. right hand side function 
              //  f=1,  f=sin(x)*sin(y), f=sin(10*x)
 func g=0;                 //  boundary condition function
 
 problem laplace(uh,vh,solver=GMRES,tgv=1e5) =   //  definion of  the problem 
    int2d(Th)( dx(uh)*dx(vh) + dy(uh)*dy(vh) ) //  bilinear form
    // +10*dx(uh)*vh,  drift term
  - int2d(Th)( f*vh )                          //  linear form
  + on(1,2,3,4,uh=g) ;                      //  boundary condition form

  laplace; // solve the problem plot(uh); // to see the result
  plot(uh,ps="Laplace.eps",value=true);

2012-06-20-c1-pic-1.png

2012-06-20-c1-pic-2.png

2012-06-20-c1-pic-3.png