


: Bibliography
: Counterexample to global existence
: Counterexample to global existence
We consider the Cauchy problem for systems of semilinear wave equations
with different propagation speeds in three space dimensions of the form
|
(1.1) |
|
|
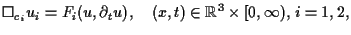 |
|
(1.2) |
|
|
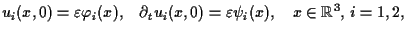 |
where
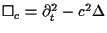 ,
,
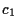 ,
, 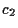 ,
,
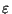 are positive constants,
are positive constants,
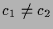 ,
and
,
and
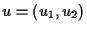 is an
is an
 -valued unknown function of
-valued unknown function of 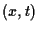 .
We assume that the nonlinear functions
.
We assume that the nonlinear functions 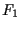 and
and 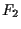 are quadratic
with respect to
are quadratic
with respect to
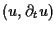 ,
and study the small data global existence and blowup for (1.1).
Here, we say that the small data global existence holds for (1.1)
if for any
,
and study the small data global existence and blowup for (1.1).
Here, we say that the small data global existence holds for (1.1)
if for any 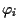 ,
,
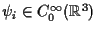
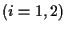 there exists a constant
there exists a constant
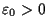 such that
for any
such that
for any
![$ \varepsilon \in (0,\varepsilon_0]$](img18.png) the Cauchy problem
(1.1)-(1.2) admits a unique global classical solution
the Cauchy problem
(1.1)-(1.2) admits a unique global classical solution
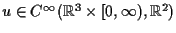 .
Moreover, we say that the small data blowup occurs
if the small data global existence does not hold.
In the present paper, we do not consider the case where
the nonlinear terms
.
Moreover, we say that the small data blowup occurs
if the small data global existence does not hold.
In the present paper, we do not consider the case where
the nonlinear terms 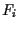 depend only on
depend only on 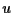 (for that case, see Kubo and Ohta [10]), and we put
(for that case, see Kubo and Ohta [10]), and we put
|
(1.3) |
 |
where
 ,
,
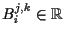 ,
, 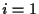 ,
, 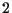 .
In what follows, we always assume that
.
In what follows, we always assume that
|
(1.4) |
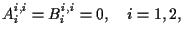 |
because it is proved by F. John [4] that
the small data blowup occurs for the single equations
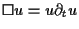 and
and
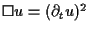 in three space dimensions
(see Klainerman [8] and Christodoulou [2]
for the small data global existence when
in three space dimensions
(see Klainerman [8] and Christodoulou [2]
for the small data global existence when 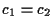 ).
).
For the case
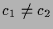 and (1.4),
the small data global existence for (1.1)
has been studied by many authors
(see, e.g., [1,3,5,6,7,9,11,12,13]).
Yokoyama [13] proved that the small data global existence
holds for (1.1) with (1.3)
if
and (1.4),
the small data global existence for (1.1)
has been studied by many authors
(see, e.g., [1,3,5,6,7,9,11,12,13]).
Yokoyama [13] proved that the small data global existence
holds for (1.1) with (1.3)
if
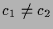 and
and
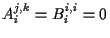 for
for 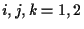 .
For the case where both
.
For the case where both  and
and  can be written in the divergent form
can be written in the divergent form
it is proved in [5] that the small data global existence
holds for (1.1) if
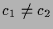 and
and
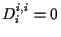 for
for 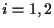 .
Moreover, Katayama [7] proved that the small data global existence
holds for (1.1) with (1.3)
if
.
Moreover, Katayama [7] proved that the small data global existence
holds for (1.1) with (1.3)
if
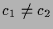 and
and
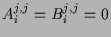 for
for  .
.
However, to our knowledge, no results on the small data blowup
have been obtained for (1.1) with (1.3)
when
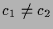 and (1.4).
The purpose in the present paper is to show that
the condition (1.4) is not sufficient to prove
the small data global existence for (1.1) with (1.3)
when
and (1.4).
The purpose in the present paper is to show that
the condition (1.4) is not sufficient to prove
the small data global existence for (1.1) with (1.3)
when
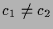 . More precisely, we consider
. More precisely, we consider
|
(1.5) |
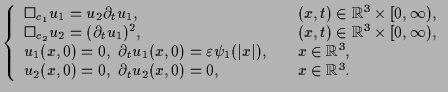 |
The main result in the present paper is as follows.
In the next section, we will give the proof of Theorem 1.1.



: Bibliography
: Counterexample to global existence
: Counterexample to global existence
Nobuki Takayama
Heisei 16-1-21.
![]() and (1.4),
the small data global existence for (1.1)
has been studied by many authors
(see, e.g., [1,3,5,6,7,9,11,12,13]).
Yokoyama [13] proved that the small data global existence
holds for (1.1) with (1.3)
if
and (1.4),
the small data global existence for (1.1)
has been studied by many authors
(see, e.g., [1,3,5,6,7,9,11,12,13]).
Yokoyama [13] proved that the small data global existence
holds for (1.1) with (1.3)
if
![]() and
and
![]() for
for ![]() .
For the case where both
.
For the case where both ![]() and
and ![]() can be written in the divergent form
can be written in the divergent form
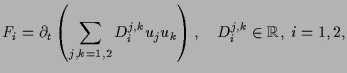
![]() and (1.4).
The purpose in the present paper is to show that
the condition (1.4) is not sufficient to prove
the small data global existence for (1.1) with (1.3)
when
and (1.4).
The purpose in the present paper is to show that
the condition (1.4) is not sufficient to prove
the small data global existence for (1.1) with (1.3)
when
![]() . More precisely, we consider
. More precisely, we consider