Introduction

A nontrivial extension of the well known difference equation

$$x_{n+1}=x_{n}+x_{n-1},\;n=0,1,2,...,$$

satisfied by the Fibonacci numbers is the following

$$x_{n+1}-x_{n}+p_{n}x_{n-k}=0,\;n=0,1,2,...$$ (1)

where $k$ is a fixed positive integer. This equation has received much attention. In particular, Erbe and Zhang [1] proved that when $\left\{ p_{n}\right\}$ is eventually nonnegative, then every solution of (1) oscillates provided

$$\limsup_{n\rightarrow \infty }\sum_{i=n-k}^{n}p_{i}>1,$$

or

$$\liminf_{n\rightarrow \infty }p_{n}>\frac{k^{k}}{(k+1)^{k+1}},$$ (2)

or

$$\liminf_{n\rightarrow \infty }p_{n}=\delta \geq 0\ \mbox{and} \ \limsup_{n\rightarrow \infty }p_{n}>1-\delta .$$

Ladas et al. in [2] obtained the same conclusion when (2) is replaced by

$$\liminf_{n\rightarrow \infty }\frac{1}{k}\sum_{i=n-k}^{n-1}p_{i}>\frac{k^{k}% }{(k+1)^{k+1}}.$$

Since then, there have been many improvements (see [1-11]). In particular, a summary of related results can be found in the recent paper [9].

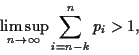
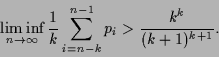
In this paper, we intend to obtain several nonstandard oscillation criteria based on the concept of frequent oscillation. Since frequent oscillation implies oscillation, our results will either be more general than or complementary to some of the results in [1-11].

In order to derive these criteria, we first recall that a real sequence is said to be oscillatory if it is neither eventually positive nor eventually negative. Clearly, such a definition does not capture the fine details of an oscillatory sequence as can be seen from the following two oscillatory sequence $\left\{ 1,-1,1,-1,...\right\}$ and $\{1,1,1,-1,1,1,1,-1,...\}$. For this reason, Tian et al. in [10] introduced the concept of frequent oscillation. For the sake of completeness, its definition and associated information will be briefly sketched as follows. Let $N=\left\{ 1,2,3,...\right\} ,$ $Z$ the set of integers and $D$ a subset of $Z$ of the form $\{a,a+1,a+2,a+3,...\}$, where $a$ is an integer. The size of a set $% \Omega$ will be denoted by $\left\vert \Omega \right\vert .$ The union, intersection and difference of two sets $A$ and $B$ will be denoted by $A+B,$ $A\cap B$ and $A\backslash B$ respectively. Let $\Omega$ be a set of integers. We will denote the set of all integers in $\Omega$ which are less than or equal to an integer $n$ by $\Omega ^{(n)},$ that is, $\Omega ^{(n)}=\Omega \cap \{...,n-1,n\},$ and we will denote the set $\{x+m\vert x\in \Omega \}$ of translates of the elements in $\Omega$ by $E^{m}\Omega ,$ where $m$ is an integer. Let $\alpha$ and $\beta$ be two integers such that $\alpha \leq \beta$. The union

$$\sigma _{\alpha }^{\beta }(\Omega )=\sum_{i=\alpha }^{\beta }E^{i}\Omega ,$$

will be called a derived set of $\Omega .$ Note that an integer $j\in E^{m}\Omega$ if and only if $j-m\in \Omega .$ Thus

$$j\in Z\backslash \left( \sigma _{\alpha }^{\beta }(\Omega )\... ...row j-k\in Z\backslash \Omega \ for\ \alpha \leq k\leq \beta .$$ (3)

Let $\Omega$ be a set of integers. If $\limsup_{n\rightarrow \infty }\left\vert \Omega ^{(n)}\right\vert /n$ exists, then this limit, denoted by $\mu ^{*}(\Omega ),$ will be called the upper frequency measure of $\Omega .$ Similarly, if $\liminf_{n\rightarrow \infty }\left\vert \Omega ^{(n)}\right\vert /n$ exists, then this limit, denoted by $\mu _{*}(\Omega ),$ will be called the lower frequency measure of $\Omega .$ If $\mu ^{*}(\Omega )=\mu _{*}(\Omega ),$ then the common limit, denoted by $\mu (\Omega ),$ will be called the frequency measure of $\Omega .$

For the sake of convenience, we will adopt the usual notation for level sets of a sequence, that is, let $x:D\rightarrow R$ be a real function, then the set $\{k\in D\vert x_{k}\leq c\}$ will be denoted by $(x\leq c)$ or $\left( x_{k}\leq c\right) .$ The notations $(x\geq c),$ $(x<c),$ etc. will have similar meanings. Let $x=\{x_{k}\}_{k=a}^{\infty }$ be a real sequence. If $% \mu ^{*}(x\leq 0)=0,$ then the sequence $x$ is said to be frequently positive. If $\mu ^{*}(x\geq 0)=0,$ then $x$ is said to be frequently negative. The sequence $x$ is said to be frequently oscillatory if it is neither frequently positive nor frequently negative. Note that if a sequence $x$ is eventually positive, then it is frequently positive; and if $x$ is eventually negative, then it is frequently negative. Thus, if it is frequently oscillatory, then it is oscillatory.

Let $x=\{x_{k}\}_{k=a}^{\infty }$ be a real sequence. If $\mu ^{*}(x\leq 0)\leq \omega ,$ then $x$ is said to be frequently positive of upper degree $% \omega .$ If $\mu ^{*}(x\geq 0)\leq \omega ,$ then $x$ is said to be frequently negative of upper degree $\omega .$ The sequence $x$ is said to be frequently oscillatory of upper degree $\omega$ if it is neither frequently positive nor frequently negative of the same upper degree $\omega .$ The concepts of frequently positive of lower degree, etc. are similarly defined by means of $\mu _{*}.$ We say that $x$ is frequently positive of the lower degree $\omega$ if $\mu _{*}(x\leq 0)\leq \omega ,$ frequently negative of the lower degree $\omega$ if $\mu _{*}(x\geq 0)\leq \omega ,$ and frequently oscillatory of lower degree $\omega$ if it is neither frequently positive nor frequently negative of the same lower degree $\omega .$ Note that if the sequence $x$ is frequently oscillatory of the lower degree $\omega ,$ then it is also frequently oscillatory of upper degree $% \omega .$ Note further that if the sequence $x$ is frequently oscillatory of upper degree $\omega$ for some $\omega>0$, then it is frequently oscillatory.

We first recall three results from [10] needed in the sequel.

LEMMA 1. Let $\Omega$ and $\Gamma$ be subsets of $D=\left\{ a,a+1,...\right\} .$ Then

$$\mu ^{*}(\Omega +\Gamma )\leq \mu ^{*}(\Omega )+\mu ^{*}(\Gamma ).$$

Furthermore, if $\Omega$ and $\Gamma$ are disjoint, then

$$\mu _{*}(\Omega )+\mu _{*}(\Gamma )\leq \mu _{*}(\Omega +\Ga... ...{*}(\Omega +\Gamma )\leq \mu ^{*}(\Omega )+\mu ^{*}(\Gamma ),$$

so that

$$\mu _{*}(\Omega )+\mu ^{*}(N\backslash \Omega )=1.$$

LEMMA 2. Let $\Omega$ and $\Gamma$ be subsets of $D=\{a,a+1,...\}$ such that $\mu ^{*}(\Omega )+\mu _{*}(\Gamma )>1.$ Then $\Omega \cap \Gamma$ cannot be a finite set.

LEMMA 3. For any subset $\Omega$ of $D=\{a,a+1,...\},$ we have

$$\mu ^{*}\left( \sigma _{\alpha }^{\beta }(\Omega )\right) \leq (\beta -\alpha +1)\mu ^{*}(\Omega ),$$

and

$$\mu _{*}\left( \sigma _{\alpha }^{\beta }(\Omega )\right) \leq (\beta -\alpha +1)\mu _{*}(\Omega ).$$