


: Bibliography
: Structure of positive solutions
: Structure of positive solutions
In this paper, we are concerned with the positive
solutions of the initial value problem (P):
| |
|
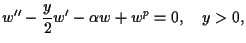 |
(1.1) |
| |
|
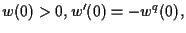 |
(1.2) |
where
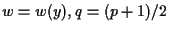 , and
, and
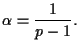 |
|
|
(1.3) |
Hereafter the prime denotes the differentiation with respect to 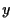 .
We always assume that
.
We always assume that 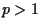 .
.
The problem (P) is closely related to
the following semilinear parabolic problem
where 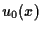 is a positive smooth function.
We say that the solution
is a positive smooth function.
We say that the solution 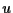 of the problem (1
1.1)-(2
1.3)
blows up if there is a finite time
of the problem (1
1.1)-(2
1.3)
blows up if there is a finite time 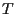 such that
such that
![$\max_{x \in [0,1]}u(x,t) \to \infty$](img13.png) as
as 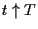 . It has been
shown by Lin and Wang [3]
that the solution
. It has been
shown by Lin and Wang [3]
that the solution  of the problem (3
1.1)-(4
1.3)
always blows up, since
of the problem (3
1.1)-(4
1.3)
always blows up, since 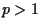 .
Also, under some conditions (for example,
.
Also, under some conditions (for example, 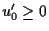 ),
), 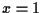 is the only
blow-up point. See [3] and [1].
is the only
blow-up point. See [3] and [1].
In order to understand the time asymptotic behaviour of  as
as
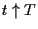 ,
we make the following well-known Giga-Kohn transformation [2]
,
we make the following well-known Giga-Kohn transformation [2]
Then the function 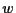 satisfies
satisfies
It is nature to expect that, as 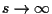 (or,
(or, 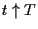 ),
), 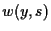 tends to a global positive solution of (P).
Therefore, the existence and uniqueness of global positive (monotone
decreasing) solution of (P) plays an important role in studying
the time asymptotic behaviour of
tends to a global positive solution of (P).
Therefore, the existence and uniqueness of global positive (monotone
decreasing) solution of (P) plays an important role in studying
the time asymptotic behaviour of  as
as 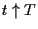 .
In fact, if
.
In fact, if  is the unique global positive monotone decreasing
solution of (P), then we have
is the unique global positive monotone decreasing
solution of (P), then we have
as 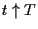 uniformly for
uniformly for ![$y \in [0,C]$](img25.png) for any
for any 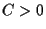 .
See [1] for more detail.
.
See [1] for more detail.
It has been proved in [4] (See also [1]) that
there is a global positive
monotone decreasing solution of (P) for any 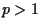 .
Also, the uniqueness of global positive monotone decreasing
solutions of (P) for
.
Also, the uniqueness of global positive monotone decreasing
solutions of (P) for ![$p \in (1,2]$](img27.png) was proved in [1].
The main purpose of this paper is to show the following theorem on the
structure of positive solutions of (P).
was proved in [1].
The main purpose of this paper is to show the following theorem on the
structure of positive solutions of (P).
We emphasize here that it follows from Theorem
5
th1 that
any solution of (P) must vanish at some finite  except the solution
starting with
except the solution
starting with  .
.
This paper is organized as follows. We first recall some facts from
[1] in §2 and derive the assertions (i) and (ii) of Theorem 1.1.
Then in §3 we prove the assertion (iii) of Theorem 1.1.
Hence the only global positive solution of (P) is the monotone
decreasing solution
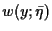 .
.



: Bibliography
: Structure of positive solutions
: Structure of positive solutions
Nobuki Takayama
Heisei 16-1-21.
![]() as
as
![]() ,
we make the following well-known Giga-Kohn transformation [2]
,
we make the following well-known Giga-Kohn transformation [2]

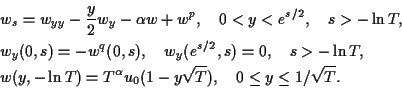
![]() .
Also, the uniqueness of global positive monotone decreasing
solutions of (P) for
.
Also, the uniqueness of global positive monotone decreasing
solutions of (P) for ![]() was proved in [1].
The main purpose of this paper is to show the following theorem on the
structure of positive solutions of (P).
was proved in [1].
The main purpose of this paper is to show the following theorem on the
structure of positive solutions of (P).
![]() .
.