


: Bibliography
: Extension of a Geometric
: Extension of a Geometric
In this paper we study the occurrence of any possible stability switch
from the increase of the value of the time delay  for general delay
equation
for general delay
equation
 |
(1.1) |
where  ,
,
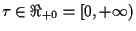 is a
fixed delay and
is a
fixed delay and 
![$(\left[ -\tau ,0\right] ,\Re
^{n})\rightarrow \Re ^{n}$](img6.png) is of class
is of class
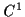 with respect both
with respect both 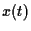 and
and 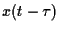 .
.
We assume that any equilibrium 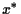 of (1.1) is delay dependent, i.e.
of (1.1) is delay dependent, i.e. 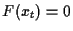 gives a constant solution
gives a constant solution
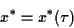 |
(1.2) |
which is continuous and differentiable in  .
.
The variation equation around 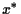 (set
(set
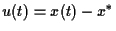 )
)
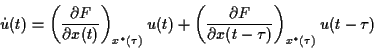 |
(1.3) |
gives the characteristic equation
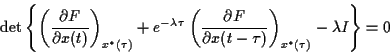 |
(1.4) |
which in general has delay dependent coefficients, where 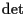 denotes the
determinant of a matrix,
denotes the
determinant of a matrix, 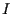 is an identity matrix and
is an identity matrix and 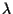 are the
corresponding characteristic roots.
are the
corresponding characteristic roots.
We give the following definition:
Definition 1.1 A stability switch occurs at
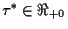 if crossing
if crossing 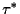 for increasing
for increasing  the stability of
the stability of 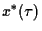 changes from asymptotic stability to instability or vice versa.
changes from asymptotic stability to instability or vice versa.
The most general structure of characteristic equation (1.4) results to be
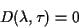 |
(1.5) |
where
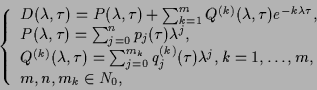 |
(1.6) |
and  ,
,
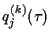 :
:
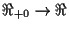 are
continuous and differentiable functions of
are
continuous and differentiable functions of
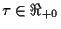 . Generally
in (1.6) is
. Generally
in (1.6) is  but herefollowing we remove this condition.
but herefollowing we remove this condition.
We assume that 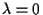 cannot be a characteristic root, i.e.
cannot be a characteristic root, i.e.
 |
(1.7) |
In the study of the occurrence of stability switches the following is an
essential result. Assume that we rewrite (1.5) as
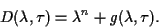 |
(1.8) |
Then, the following theorem holds (see Freedman and Kuang [5]):
It is to be noticed that if in (1.6)
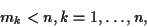 |
(1.10) |
i.e. the degree of polynomial 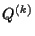 in
in 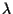 is lower than the
degree
is lower than the
degree 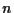 polynomial
polynomial 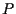 in
in 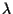 , then assumption (1.9) holds true
and Theorem 1.1 applies to the characteristic equation (1.5) and (1.6).
, then assumption (1.9) holds true
and Theorem 1.1 applies to the characteristic equation (1.5) and (1.6).
Rewrite
 in (1.6) like
in (1.6) like
without loss of generality we assume
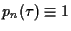 and define
and define
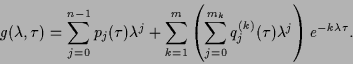 |
(1.11) |
Assume 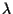 such that
such that
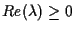 . Then, for any
. Then, for any 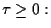
since on the right hand side of (1.12) 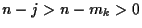 . Therefore, the
assumption (1.9) of the Theorem 1.1 holds true. Hence, characteristic
equations (1.5) with structure (1.6) which satisfy (1.7) and (1.10), i.e.
. Therefore, the
assumption (1.9) of the Theorem 1.1 holds true. Hence, characteristic
equations (1.5) with structure (1.6) which satisfy (1.7) and (1.10), i.e.
may have a stability switch for some 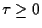 , say
, say 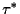 , only if
, only if

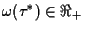 are
characteristic roots.
are
characteristic roots.
In the following of the paper we still study the occurrence of stability
switches for the subclass of characteristic equations (1.5) where
 |
(1.13) |
which is already sufficiently general to include as a particular case the
characteristic equation
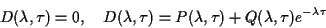 |
(1.14) |
recently studied by Beretta and Kuang [3]. An application is also shown in
a paper by Beretta, Carletti and Solimano [2].
Therefore, we extend the geometric stability switch criterion
developed by Beretta and Kuang [3] for (1.14) to the more general case
(1.13). This will be done in the next section.
However, we don't feel that the method we are presenting in the next section
could be applied to general characteristic equations (1.6) with 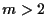 .
.
In Section 3 we present an application of the geometric stability switch
criterion.
We conclude the paper with Section 4 showing that many of the characteristic
equations known in literature are included in the case with structure
(1.13), and that related stability switch results are obtained as particular
cases of the geometric stability switch criterion presented in Section 2.



: Bibliography
: Extension of a Geometric
: Extension of a Geometric
Nobuki Takayama
Heisei 16-1-21.
![]() of (1.1) is delay dependent, i.e.
of (1.1) is delay dependent, i.e. ![]() gives a constant solution
gives a constant solution
![]() (set
(set
![]() )
)
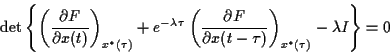
![]() if crossing
if crossing ![]() for increasing
for increasing ![]() the stability of
the stability of ![]() changes from asymptotic stability to instability or vice versa.
changes from asymptotic stability to instability or vice versa.
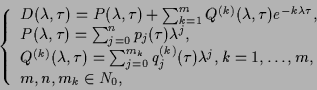
![]() cannot be a characteristic root, i.e.
cannot be a characteristic root, i.e.
![]() in (1.6) like
in (1.6) like
![\begin{displaymath}
D(\lambda ,\tau )=p_{n}(\tau )\lambda ^{n}+\left[ \sum_{j=0}...
...{j}^{(k)}(\tau
)\lambda ^{j}\right) e^{-k\lambda \tau }\right]
\end{displaymath}](img41.png)
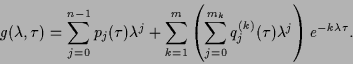
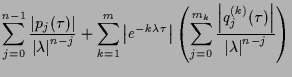
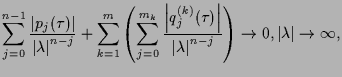
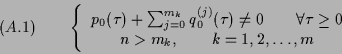
![]() .
.