Introduction

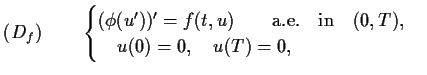
In this paper we study the boundary value problem

$$(D_f)\quad\quad\begin{cases}(\phi(u'))'=f(t,u) \qquad\text{a.e.}\quad \mbox{in}\quad(0,T), \\ \quad u(0)=0,\quad u(T)=0, \end{cases}$$

where $\phi$ is a homeomorphism from ${\mathbb{R}}^N$ onto ${\mathbb{R}}^N$ and the function $f:I\times{\mathbb{R}}^N\to {\mathbb{R}}^N$ is assumed to be Carathéodory. Here $I:=[0,T]$ and $':=\frac{d}{dt}.$

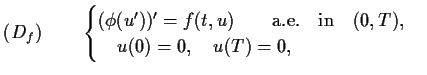
By a solution of $(D_f)$ we understand a function $u:I\to{\mathbb{R}}^N$ of class $C^1$ with $\phi(u')$ absolutely continuous, which satisfies $(D_f).$

In most of the paper we shall ask $\phi$ to satisfy the following conditions:

($H_1$)

For any $x_1,x_2\in {\mathbb{R}}^N,$ $x_1\not=x_2,$

$$\langle \phi(x_1)-\phi (x_2), x_1-x_2 \rangle>0.$$

($H_2$)

There exists a function $\rho:[0,+\infty[\to [0,+\infty[$ such that $\rho(s)\to +\infty$ as $s\to +\infty$ and

$$\langle \phi(x),x \rangle \,\ge \,\rho(\vert x\vert)\vert x\vert,$$   for all  $$x\in {\mathbb{R}}^N.$$

In $(H_1)$ and $(H_2),$ as in the rest of the paper, $\langle\cdot,\cdot\rangle$ denotes the inner product and $\vert\cdot\vert$ the Euclidean norm in ${\mathbb{R}}^N$. Throughout the paper $\vert\cdot\vert$ will also denote the absolute value in ${\mathbb{R}}.$

It is well known that conditions $(H_1)$ and $(H_2)$ ensure that $\phi$ is a homeomorphism from ${\mathbb{R}}^N$ onto ${\mathbb{R}}^N.$ The vector version of the $p-$Laplace operator, namely the case when for $x=(x_1,\cdots,x_N)\in{\mathbb{R}}^N,$

$$\quad \phi(x)=\psi_p(x)\equiv \vert x\vert^{p-2}x, \quad x \neq 0,\quad\psi_p(0) = 0,\;p>1,$$ (1.1)

as well as the cases

$$\phi(x)=\vert x\vert^{p-2}x\log(1+\vert x\vert),\quad p>1,\quad x\in{\mathbb{R}}^N,$$ (1.2)

$$\phi(x)=\vert x\vert^{p-2}x+\vert x\vert^{q-2}x,\quad 1<q<p,\quad x\in{\mathbb{R}}^N,$$ (1.3)

satisfy conditions $(H_1)$ and $(H_2).$ Further examples of functions satisfying these conditions can be found in [8].

When $N=1$ it can be checked that the function $\phi$ as given in examples (1.1), (1.2) and (1.3) also satisfy the property

$$\displaystyle \lim\limits_{\vert s\vert\to\infty}\frac{\phi(\sigma s)}{\phi(s)}~=~\sigma^{p-1} \qquad \mbox{for all} \ \sigma > 0.$$ (1.4)

In the scalar case, functions $\phi$ satisfying (1.4) have been called asymptotically homogeneous functions, see [1], [4], [5] and [6], where they were used in connection with the existence of solutions to quasilinear elliptic problems. They form an important class of non-homogeneous functions satisfying a suitable homogeneous behavior at infinity (or zero) without being necessarily asymptotic to any power at infinity or zero.

As we said before the function $f:I\times{\mathbb{R}}^N\to {\mathbb{R}}^N$ is assumed to be Carathéodory. This means that $f$ satisfies the following conditions:

($C_1$)

for almost every $t\in I$ the function $f(t,\cdot)$ is continuous;

($C_2$)

for each $x\in{\mathbb{R}}^N$ the function $f(\cdot,x)$ is measurable on $I$;

($C_3$)

for each $m>0$ there is $\rho_m\in L^1(I,{\mathbb{R}})$ such that, for almost every $t\in I$ and every $x\in{\mathbb{R}}^N$ with $\vert x\vert\le m,$ one has

$$\vert f(t,x)\vert\le \rho_m(t).$$

In case $f:I\times{\mathbb{R}}^N\times [0,1]\to {\mathbb{R}}^N$ (mapping $(t,x,\lambda)$ into $f(t,x,\lambda)$), we shall say $f$ is Carathéodory, if ($C_1$) and ($C_2$) are satisfied for each $\lambda\in [0,1]$ and the function $\rho_m$ in ($C_3$) can be chosen independently of $\lambda\in [0,1]$, i.e.,

$$\vert f(t,x,\lambda)\vert\le \rho_m(t)$$   for a.e$$\ t\in I, \$$   all$$\ \lambda\in [0,1] \$$   and all$$\ \vert x\vert\le m.$$

We state a piece of notations used in this paper. For $N\ge 1$ we shall set $C= C(I,{\mathbb{R}}^N),$ $C^1= C^1(I,{\mathbb{R}}^N),$ $C_0=\{u\in C~\vert~u(0)=0,\, u(T)=0\},$ $C_0^1=\{u\in C^1~\vert~u(0)=0,\,u(T)=0\}.$ The norm in $C$ and $C_0$ will be denoted by $\vert\vert\cdot\vert\vert,$ while the norm in $C^1_0$ by $\vert\vert\cdot\vert\vert _{C^1_0}.$ $L^p=L^p((0,T),{\mathbb{R}}),$ $L^p_N=\prod_{i=1}^NL^p((0,T),{\mathbb{R}}),$ $p\ge 1.$

This paper is organized as follows. In section 2 we extend the concept of Asymptotically Homogeneous functions from the scalar to the vector case, and study some of their properties. In particular it is seen how this family is related to the vector $p$-Laplace function $\vert u\vert^{p-2}u$ at infinity.

In section 3 we study the eigenvalues of the weighted eigenvalue problem of the form

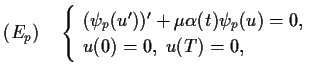$$(E_p)\quad\begin{cases} ~(\psi_p(u'))' + \mu\alpha(t) \psi_p(u) = 0,\cr~~ u(0) = 0, \; u(T) =0, \end{cases}$$ (1.5)

where $\alpha$ is positive a.e. and belongs to $L^1.$ This is a key result to be used in later sections. Together with this result we also show in this section that an associated initial value problem has a unique solution.

In section 4 we give our first existence result for a system of ode's, under Dirichlet boundary conditions, containing a quasilinear operator generated by a vector function which is Asymptotically Homogeneous at infinity.

Section 5 is dedicated to the study of a system of ode's whose quasilinear operator is not Asymptotically Homogeneous, but its components are. A simple example of this situation is given by the function $\bigl(\vert x_1\vert^{p_1-2}x_1,$ $\cdots, \vert x_N\vert^{p_N-2}x_N\bigr),$ which is not Asymptotically Homogeneous at infinity. We prove in this section our second existence result for a system of ode's, with Dirichlet boundary conditions, containing this type of quasilinear operator.

Finally in Section 6, we give some examples of vector functions which are Asymptotically Homogeneous at infinity.