Introduction

Let ${}_p F_{p-1}(a_1, \ldots, a_p, b_2, \ldots, b_p; z)$ be the generalized hypergeometric function

$$\sum_{n=0}^\infty \frac{(a_1)_n \cdots (a_p)_n} {(1)_n (b_2)_n \cdots (b_p)_n} z^n, \quad (a)_n = a(a+1) \cdots (a+n-1).$$

Theorem 1.1   The generalized hypergeometric function ${}_p F _{p-1}$ satisfies the following quadratic relation

$$\sum_{i=1, j=1}^{p} \left( \theta^{i-1} {}_p F_{p-1}(A,B;z) \right) \frac{c_{ij}}{c_{11}} \left( \theta^{j-1} {}_p F_{p-1}(-A,2-B;z) \right) = 1$$ (1)

for generic values of parameters $a_i$ and $b_j$ where $\theta = zd/dz$, $A=(a_1, \ldots, a_p)$, $B=(b_2, \ldots, b_p)$, $-A=(-a_1, \ldots, -a_p)$, $2-B=(2-b_2, \ldots, 2-b_p)$. The number $c_{ij}$ is the $(i,j)$-element of the transposed inverse of the intersection matrix of cocycles associated to ${}_p F _{p-1}$ and the intersection matrix is inductively determined with respect to $p$ by the formula given in Theorem 8.2. For example, these relations for $p=2, 3$ are as follows.
(a) $p=2$

$$\ {}_2F_1(a_1, a_2, b_2;z) \, {}_2F_1(-a_1,-a_2,2-b_2;z)$$

$$+ \frac{z}{e_2}\, {}_2F_1'(a_1, a_2, b_2;z) \, {}_2F_1(-a_1,-a_2,2-b_2;z)$$

$$- \frac{z}{e_2}\, {}_2F_1(a_1, a_2, b_2;z) \, {}_2F_1'(-a_1,-a_2,2-b_2;z)$$

$$- \frac{a_1+a_2-e_2}{a_1 a_2 e_2}z^2\, {}_2F_1'(a_1, a_2, b_2;z)\,{}_2F_1'(-a_1,-a_2,2-b_2;z) = 1$$

where $e_2 = b_2-1$ and $a_1 a_2 \not= 0, e_2, % \not\in {\bf Z}$.
(b) $p=3$

$$\, {}_3 F_2 (A,B;z)\, {}_3 F_2 (-A,2-B;z)$$

$$+ \frac{(-t_1+1) z}{t_2}\, {}_3 F_2 (A,B;z)\, {}_3 F_2 '(-A,2-B;z)$$

$$+ \frac{z^2}{t_2}\, {}_3 F_2 (A,B;z)\, {}_3 F_2 ''(-A,2-B;z)$$

$$+ \frac{(t_1+1) z}{t_2}\, {}_3 F_2 '(A,B;z)\, {}_3 F_2 (-A,2-B;z)$$

$$+ \frac{((t_2+1) s_1-t_1 s_2-s_3-t_1) z^2}{t_2 s_3}\, {}_3 F_2 '(A,B;z)\, {}_3 F_2 '(-A,2-B;z)$$

$$+ \frac{(s_1+s_2-t_1-t_2) z^3}{t_2 s_3}\, {}_3 F_2 '(A,B;z)\, {}_3 F_2 ''(-A,2-B;z)$$

$$+ \frac{z^2}{t_2}\, {}_3 F_2 ''(A,B;z)\, {}_3 F_2 (-A,2-B;z)$$

$$+ \frac{(s_1-s_2-t_1+t_2) z^3}{t_2 s_3}\, {}_3 F_2 ''(A,B;z)\, {}_3 F_2 '(-A,2-B;z)$$

$$+ \frac{(s_1-t_1) z^4}{t_2 s_3}\, {}_3 F_2 ''(A,B;z)\, {}_3 F_2 ''(-A,2-B;z)$$

$$= 1$$

where $s_1 = a_1+a_2+a_3$, $s_2 = a_1 a_2 + a_2 a_3 + a_3 a_1$, $s_3 = a_1 a_2 a_3$, $t_1 = e_2+e_3$, $t_2 = e_2 e_3$, $e_2 = b_2-1, e_3 = b_3-1$, and $A=(a_1,a_2,a_3,a_4)$, $B=(b_2,b_3,b_4)$, $-A=(-a_1,-a_2,-a_3,-a_4)$, $2-B=(2-b_2,2-b_3,2-b_4)$. Parameters must satisfy the condition $a_1 a_2 a_3 \not= 0, b_2, b_3 \not\in {\bf Z} %$.

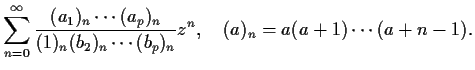
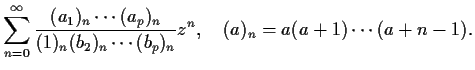
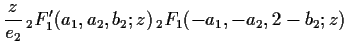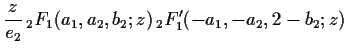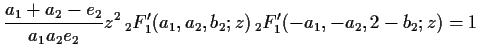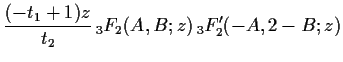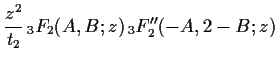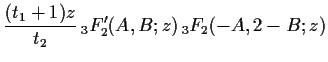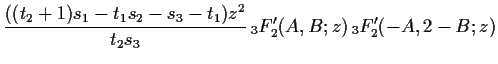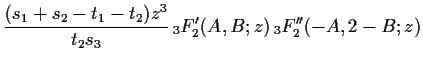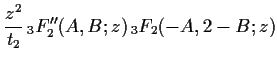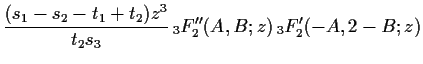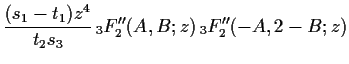Some identities for hypergeometric functions have geometric meaning behind. Aomoto proposed a method to study hypergeometric functions as pairings of cycles and cocycles about 30 years ago [1]. This ingenious point of view has enabled us to yield a lot of formulas for hypergeometric functions.

The identities we have presented above are quadratic relations for ${}_p F _{p-1}$. We will see that it also has a geometric meaning based on a work of Cho and Matsumoto. They proved an analog of Riemann's period relation for intersection numbers of cycles and cocycles and associated period integral, of which entries are nothing but hypergeometric functions [2]. The period relation yields a quadratic relation of hypergeometric functions. Therefore, the problem of deriving quadratic relations is reduced to evaluation of intersection numbers. Cho, Kita, Matsumoto and Yoshida gave formulas to evaluate intersection numbers for a class of hypergeometric functions expressed by a definite integral of which integrant has a normally crossing singular locus [2], [5], [6], [7]. The GHF ${}_p F _{p-1}$ has a multiple integral representation on ${\bf C}^{p-1}$ but the singular locus of the integrant is not normally crossing. Hence, the generalized hypergeometric functions are out of the class for general $p$, because their method requires a construction of resolutions of singularities and it is difficult in general. We will introduce a different approach to study the GHF. The GHF is expressed in terms of the single integral

$$\frac{\Gamma(a_p)\Gamma(b_p-a_p)} {\Gamma(b_p)} \,{}_pF_{p-1}(a_1, \ldots, a_p, b_2, \ldots, b_p;z)$$

$$= z^{-b_p+1} \int_0^z t^{a_p} (z-t)^{b_p -1- a_p} \,{}_{p-1}F_{p-2}(a_1, \ldots, a_{p-1}, b_2, \ldots, b_{p-1};z) \frac{dt}{t}$$

The kernel function ${}_{p-1} F_{p-2}$ defines a locally constant sheaf of which rank is $p-1$. We will evaluate intersection numbers by utilizing this integral representation. Cho, Kita, Matsumoto and Yoshida's formulas are those for locally constant sheaves associated to a product of linear forms, which are rank one sheaves. The kernel function ${}_{p-1} F_{p-2}$ defines a locally constant sheaf of which rank is more than $1$. Hence, we cannot apply their formulas to the single integral representation of ${}_p F _{p-1}$.

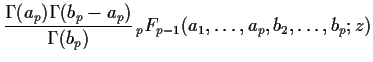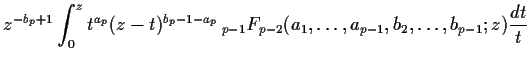The first author studied a method to evaluate intersection numbers for cocycles with coefficients in locally constant sheaves of which rank is more than one. He applied the method for evaluating intersection numbers for cocycles associated to the Selberg type integrals [9], [10].

In this paper, we first reexamine the definition of intersection number in view of the topological cup product, because discussions by Kita and Yoshida [5] are not satisfactory to apply for our problem of ${}_p F _{p-1}$ and those by the first author in [10] are not satisfactory to be a rigorous foundation. We will see that the method of the first author in [9], [10] is not only useful for computation, but also is a consequence of a general theory of duality. Next, we apply the method to evaluate intersection numbers for ${}_p F _{p-1}$. The twisted cohomology and homology groups associated to the single integral representation of ${}_p F _{p-1}$ are direct sums of primary parts and degenerate parts. Only the primary parts stand for ${}_p F _{p-1}$ [8]. This degeneration makes the evaluation of intersection numbers more complicated than the evaluation problem for the Selberg type integrals.