


: この文書について...
: On a class of
: Introduction
- 1
-
F. V. Andreev and A. V. Kitaev,
Transformations
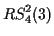 of the ranks
of the ranks 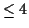 and algebraic
solutions of the sixth Painlevé equation,
preprint, nlin.SI/0107074.
and algebraic
solutions of the sixth Painlevé equation,
preprint, nlin.SI/0107074.
- 2
-
B. Dubrovin and M. Mazzocco,
Monodromy of certain Painleve VI transcendents and reflection groups,
Invent. Math. 141 (2000) 55-147.
- 3
-
N. J. Hitchin,
Poncelet polygons and the Painlevé equations,
Geometry and analysis (Bombay, 1992) 151-185,
Tata Inst. Fund. Res., Bombay, 1995.
- 4
-
K. Iwasaki, H. Kimura, S. Shimomura and M. Yoshida,
From Gauss to Painlevé - A Modern Theory of Special Functions,
Aspects of Mathematics E16, Vieweg, 1991.
- 5
-
K. Kajiwara and T. Masuda,
On the Umemura polynomials for the Painlevé III equation,
Phys. Lett. A 260 (1999) 462-467.
- 6
-
K. Kajiwara, T. Masuda, M. Noumi, Y. Ohta and Y. Yamada,
Determinant formulas for the Toda and discrete Toda equations,
Funkcial. Ekvac. 44 (2001) 291-307.
- 7
-
K. Kajiwara and Y. Ohta,
Determinant structure of the rational solutions for the Painlevé II equation,
J. Math. Phys. 37 (1996) 4693-4704.
- 8
-
K. Kajiwara and Y. Ohta,
Determinant structure of the rational solutions for the Painlevé IV equation,
J. Phys. A: Math. Gen. 31 (1998) 2431-2446.
- 9
-
A. N. Kirillov and M. Taneda,
Generalized Umemura polynomials,
to appear in Rocky Mountain Journal of Mathematics, math.CO/0010279.
- 10
-
A. N. Kirillov and M. Taneda,
Generalized Umemura polynomials and Hirota-Miwa equations,
to appear in MSJ Memoirs, math.CO/0106025.
- 11
-
K. Koike,
On the decomposition of tensor products of the representations of the classical groups:
by means of the universal characters,
Adv. Math. 74 (1989) 57-86.
- 12
-
T. Masuda, Y. Ohta and K. Kajiwara,
A determinant formula for a class of rational solutions of Painlevé V equation,
to appear in Nagoya Math. J. 168 (2002), nlin.SI/0101056.
- 13
-
M. Mazzocco,
Picard and Chazy solutions to the Painlevé VI equation,
Math. Ann. 321 (2001) 157-195.
- 14
-
M. Mazzocco,
Rational solutions of the Painlevé VI equation,
J. Phys. A: Math. Gen. 34 (2001) 2281-2294.
- 15
-
M. Noumi, S. Okada, K. Okamoto, and H. Umemura,
Special polynomials associated with the Painleve equations II,
In: Saito, M. H., Shimizu, Y., Ueno, K. (eds.)
Proceedings of the Taniguchi Symposium, 1997,
Integrable Systems and Algebraic Geometry.
Singapore: World Scientific, 1998, pp. 349-372.
- 16
-
M. Noumi and Y. Yamada,
Symmetries in the fourth Painlevé equation and Okamoto polynomials,
Nagoya Math. J. 153 (1999) 53-86.
- 17
-
M. Noumi and Y. Yamada,
Umemura polynomials for the Painlevé V equation,
Phys. Lett. A247 (1998) 65-69.
- 18
-
M. Noumi and Y. Yamada,
Higher order Painlevé equations of type
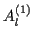 ,
Funkcial. Ekvac. 41 (1998) 483-503.
,
Funkcial. Ekvac. 41 (1998) 483-503.
- 19
-
M. Noumi and Y. Yamada,
Affine Weyl groups, discrete dynamical systems and Painlevé equations,
Commun. Math. Phys. 199 (1998) 281-295.
- 20
-
M. Noumi and Y. Yamada,
A new Lax pair for the sixth Painlevé equation associated with
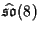 ,
to appear in Microlocal Analysis and Complex Fourier Analysis,
World Scientific, math-ph/0203029.
,
to appear in Microlocal Analysis and Complex Fourier Analysis,
World Scientific, math-ph/0203029.
- 21
-
K. Okamoto,
Studies on the Painlevé equations I,
sixth Painlevé equation P
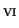 ,
Annali di Matematica pura ed applicata CXLVI (1987) 337-381.
,
Annali di Matematica pura ed applicata CXLVI (1987) 337-381.
- 22
-
K. Okamoto,
Studies on the Painlevé equations II,
fifth Painlevé equation P
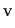 ,
Japan J. Math. 13 (1987) 47-76.
,
Japan J. Math. 13 (1987) 47-76.
- 23
-
K. Okamoto,
Studies on the Painlevé equations III,
second and fourth Painlevé equations, P
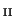 and P
and P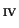 ,
Math. Ann. 275 (1986) 222-254.
,
Math. Ann. 275 (1986) 222-254.
- 24
-
K. Okamoto,
Studies on the Painlevé equations IV,
third Painlevé equation P
 ,
Funkcial. Ekvac. 30 (1987) 305-332.
,
Funkcial. Ekvac. 30 (1987) 305-332.
- 25
-
P. Painlevé,
Sur les équations différentielles du second ordre à points critiques fixes,
C. R. Acad. Sci. Paris 143 (1906) 1111-1117.
- 26
-
M. Taneda,
Polynomials associated with an algebraic solution of the sixth Painlevé equation,
to appear in Jap. J. Math. 27 (2002).
- 27
-
H. Umemura,
Special polynomials associated with the Painlevé equations I,
preprint.
- 28
-
A. P. Vorob'ev,
On rational solutions of the second Painlevé equation.
Diff. Uravn. 1 (1965) 58-59.
- 29
-
Y. Yamada,
Determinant formulas for the
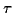 -functions of the Painlevé equations of type
-functions of the Painlevé equations of type 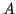 ,
Nagoya Math. J. 156 (1999) 123-134.
,
Nagoya Math. J. 156 (1999) 123-134.
Nobuki Takayama
Heisei 15-5-31.