Introduction.

Consider the linear difference system including $N$ delays

$$y_{n+1}-y_{n}+ A\sum_{j=1}^{N}y_{n-k_{j}}=0, \quad n\in {\bf Z}_{+}=\{0,1,2,\ldots\}, \eqno(1.1)$$

where $A$ is a real $m\times m$ constant matrix and the delays $k_{j}\,(j=1,\ldots,N)$ are positive integers satisfying the conditions $k_{1}\leq k_{2}\leq \cdots \leq k_{N}$. Here we assume that the sequence $\{k_{j}\}$ is arithmetic, that is,

$$k_{j+1}=k_{j}+ d,\qquad j=1,2,\ldots,N-1$$

hold for some nonnegative integer $d$. We are concerned with the asymptotic stability of the system (1.1). Furthermore, we are concerned with the asymptotic periodic behavior of solutions when the system meets some critical conditions. Here we call that a linear system is asymptotically stable if all solutions of the system approach the zero solution as $n$ tends to infinity.

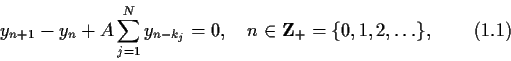
By an appropriate linear transformation, we can obtain from (1.1) a system whose coefficient matrix is given in a Jordan form. Thus it is sufficient to discuss the problems above for the two-dimensional system

$$x_{n+1}-x_{n}+ B\sum_{j=1}^{N}x_{n-k_{j}}=0, \qquad n\in {\bf Z}_{+}, \eqno(1.2)$$

where $B$ is a $2\times 2$ matrix given by either

$${\rm (i)} \ \ \ p\left( \begin{array}{lr} \cos{\theta} & ... ...1} & q \\ 0 & p_{2} \end{array}\right) \qquad \qquad \qquad$$

with real constants $p,\,\theta,\ p_{1},\,p_{2}$, $q$, and $\theta$ satisfying $0<\vert\theta\vert\leq \pi/2$.

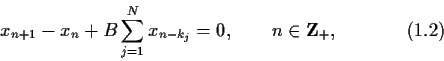
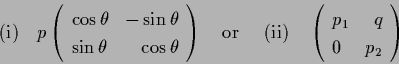
Recently, Matsunaga and Hara [5] (in the case of $N=1$) and then the author [7] (in the case of $N=2$) obtained necessary and sufficient conditions for (1.2) to be asymptotically stable. Their results can be viewed as generalizations of the well-known criterion due to Levin and May [4] (see also [3,10]) for the scalar difference equation which originally appeared in mathematical biology:

$$u_{n+1}-u_{n}+ pu_{n-k}=0, \qquad n\in {\bf Z}_{+}.$$

Also, Ogita et.al.[9] considered the scalar equation corresponding to (1.2):

$$u_{n+1}-u_{n}+ p\sum_{j=1}^{N}u_{n-k_{j}}=0, \qquad n\in {\bf Z}_{+} \eqno(1.3)$$

and gave a necessary and sufficient condition for the asymptotic stability, when $\{k_{j}\}$ is arithmetic.

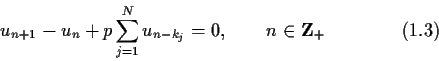
The first purpose of this paper is to establish necessary and sufficient conditions for (1.2) to be asymptotically stable, which are described explicitly in terms of the components of $B$ and the delays $\{k_{j}\}$ and our results extend ones mentioned above [4,5,7,9].

In addition, we investigate the behavior of solutions of (1.2) in the critical case where the system loses its asymptotic stability. In such a case, numerical simulations seem to show that every solution approaches some periodic solution depending on its initial data as $n$ tends to infinity. Actually, the author [8] proved such an asymptotic periodic behavior of solutions of (1.2) with $N=1$, and obtained explicit representations of those periodic solutions in the critical case. Related to this kind of problem, Matsunaga et.al [6] studied the asymptotic periodicity and the asymptotic constancy for a certain type of linear difference systems with one delay. The second purpose of this paper is to discuss the asymptotic periodicity of (1.2) for general $N$ when the system is critical in the above sense.

This paper is outlined as follows: In section 2 we state our main results for asymptotic stability, give their proofs and also discuss the asymptotic stability condition of (1.1). In section 3 we prove that solutions of (1.2) show asymptotic periodic behavior in the critical case and moreover we give explicit expressions of those periodic solutions.