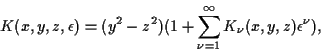: Bibliography
: Approximations of the Relativistic
: Approximations of the Relativistic
In [2] we investigated the Cauchy problem to the relativistic
Euler equation
Here 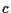 is a positive constant, the speed of light,
and
is a positive constant, the speed of light,
and 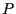 is a given smooth function of
is a given smooth function of 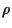 satisfying the
assumption
satisfying the
assumption
(A):
 for
for 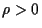 , and
, and
|
(1) |
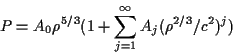 |
as
 . Here
. Here  is a positive constant
and
is a positive constant
and 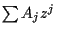 is a power series with positive radius of convergence.
is a power series with positive radius of convergence.
In order to prove the existence of global weak solutions
to the Cauchy problem by the theory of compensated compactness,
we have to solve the relativistic Euler-Poisson-Darboux
equation
where the independent variables are
|
(2) |
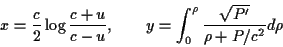 |
and the unknown function 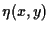 is an entropy to
is an entropy to 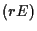 .
The coefficients of
.
The coefficients of 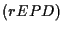 are given by
are given by
By the definition (2) and the assumption (1), we see
that 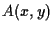 and
and  are of the form
are of the form
Here and hereafter we denote
|
(3) |
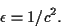 |
Introducing the new unknown  by
by
|
(4) |
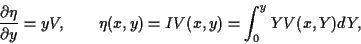 |
the singularity of 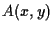 in
in 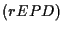 can be eliminated
and
can be eliminated
and 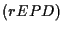 is reduced to the equation
is reduced to the equation
The problem
admits a unique solution  for any smooth
for any smooth 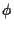 given by a
formula
given by a
formula
|
(5) |
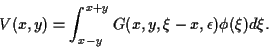 |
For the proof see [2], Section 5.
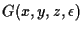 is a smooth
function of
is a smooth
function of
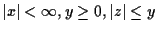 .
Therefore by defining
.
Therefore by defining
|
(6) |
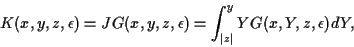 |
we have a formula
|
(7) |
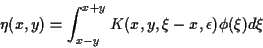 |
for solutions of 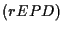 .
We call this formula
the relativistic Darboux formula and
.
We call this formula
the relativistic Darboux formula and 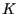 the
relativistic Darboux kernel.
We know
the
relativistic Darboux kernel.
We know
|
(8) |
 |
The purpose of this article is to study the properties of this
relativistic Darboux kernel.
The motivations are as follows.
First we see that
 tends to the Darboux kernel
tends to the Darboux kernel
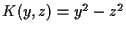 as
as 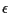 tends to
tends to 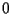 . Therefore the
solution
. Therefore the
solution 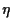 of
of 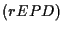 tends to those of the Euler-Poisson-Darboux
equation
tends to those of the Euler-Poisson-Darboux
equation
as 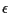 tends to
tends to 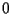 .
But
.
But 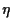 is an entropy and there is a gap between the convergence
of entropies and the convergence of solutions
is an entropy and there is a gap between the convergence
of entropies and the convergence of solutions 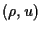 of
the Euler equation.
We conjecture that weak solutions to
of
the Euler equation.
We conjecture that weak solutions to 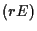 contain
a subsequence which converges to a weak solution of
the non-relativistic Euler equation
contain
a subsequence which converges to a weak solution of
the non-relativistic Euler equation
as
 tends to
tends to 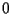 . Actually
this is the case if we assume
. Actually
this is the case if we assume 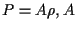 being a constant
being a constant 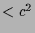 , since
the total variations of the solutions obtained by Glimm's scheme
in [5] can be
estimated uniformly with respect to
, since
the total variations of the solutions obtained by Glimm's scheme
in [5] can be
estimated uniformly with respect to 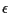 . See [4] for a proof.
But this conjecture is not yet proved if we assume a more realistic equation of
states (A). In order to approach this problem it is necessary
to give a particuler account of the dependence of
. See [4] for a proof.
But this conjecture is not yet proved if we assume a more realistic equation of
states (A). In order to approach this problem it is necessary
to give a particuler account of the dependence of 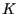 upon
upon 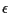 .
We want to find the first order term of the expansion
of
.
We want to find the first order term of the expansion
of 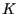 with respect to
with respect to 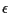 .
Using such detailed informations, we might discuss the properties of
weak solutions to the equation with the parameter
.
Using such detailed informations, we might discuss the properties of
weak solutions to the equation with the parameter 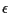 which are obtained by the compensated compactness method.
Maybe a general theory cannot be expected
and we must consider according to the situations.
Second although we can guarantee the existence of weak solutions
for any bounded initial data
which are obtained by the compensated compactness method.
Maybe a general theory cannot be expected
and we must consider according to the situations.
Second although we can guarantee the existence of weak solutions
for any bounded initial data
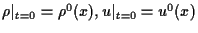 such that
such that
provided that
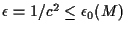 ,
,
 being a positive number depending upon
being a positive number depending upon
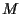 , but what happens if
, but what happens if
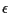 is not so small and
is not so small and 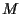 is large?
Observing the proof of [2], we find that
we use the fact that
is large?
Observing the proof of [2], we find that
we use the fact that
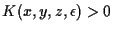 on the considered region in which
on the considered region in which
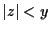 . Thus we wonder whether
. Thus we wonder whether 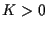 if
if
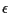 is not so small and
is not so small and  are large.
In other words the global behavior of the kernel
are large.
In other words the global behavior of the kernel
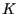 is of interest.
In order to consider this problem,
we also should give a particular account of the
dependence of
is of interest.
In order to consider this problem,
we also should give a particular account of the
dependence of 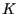 upon
upon 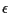 .
These are the motivations of this study.
.
These are the motivations of this study.
The conclusions of the present study are
Theorem 1
The relativistic Darboux kernel
 is analytic in
is analytic in
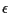 and
where
and
where
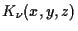 is a homogeneous polynomial of
is a homogeneous polynomial of
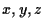 of order
of order  of the form
The power series is convergent for
of the form
The power series is convergent for
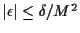 ,
where
,
where
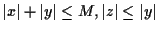 and
and
 is a positive constant.
Particularly
is a positive constant.
Particularly
Theorem 2
The relativistic Darboux kernel
 is approximated
by
is approximated
by
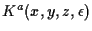 given in the following manner.
If
given in the following manner.
If 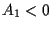 , then
If
, then
If 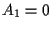 , then
If
, then
If 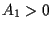 , then
Here
, then
Here 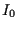 is the modified Bessel function of order 0,
is the modified Bessel function of order 0,
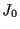 is the Bessel function of order 0,
is the Bessel function of order 0,
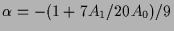 ,
,
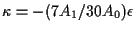 and for any smooth
and for any smooth 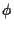 the function
satisfies the equation
which is congruent with (rEPD) modulo
the function
satisfies the equation
which is congruent with (rEPD) modulo 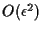 .
.



: Bibliography
: Approximations of the Relativistic
: Approximations of the Relativistic
Nobuki Takayama
Heisei 15-5-31.
![]() for
for ![]() , and
, and
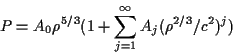
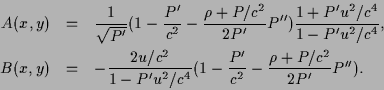
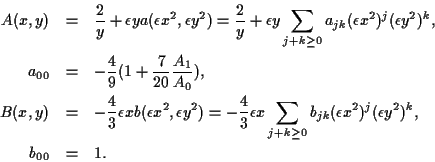
![]() tends to the Darboux kernel
tends to the Darboux kernel
![]() as
as ![]() tends to
tends to ![]() . Therefore the
solution
. Therefore the
solution ![]() of
of ![]() tends to those of the Euler-Poisson-Darboux
equation
tends to those of the Euler-Poisson-Darboux
equation