


Next: Bibliography
Up: On White Hole Solutions
Previous: On White Hole Solutions
Consider the nonlinear ordinary differential equation
where
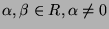 , are constants and
, are constants and
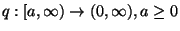 , is a continuous function.
By a solution of (A) on an interval
, is a continuous function.
By a solution of (A) on an interval
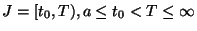 , we mean a function
, we mean a function 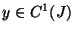 which has the property
which has the property
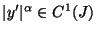 and satisfies (A) at each point of
and satisfies (A) at each point of 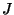 . If we
denote by
. If we
denote by 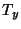 the maximal existence time of
the maximal existence time of 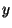 , then we say that
, then we say that 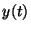 is proper if
is proper if 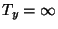 and
and
A solution 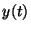 is called singular if either
is called singular if either 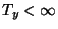 or
or 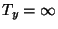 and there exists
and there exists
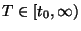 such that
such that
and  for
for 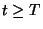 . In the later case, the interval
. In the later case, the interval  is
called the support of the solution
is
called the support of the solution 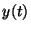 .
.
Our main objective here is to investigate the structure of the solution set of
(A) in the case 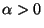 and to show that nonlinear equations of the
form (A) may have singular
solutions of a new type satisfying
and to show that nonlinear equations of the
form (A) may have singular
solutions of a new type satisfying
at the (finite) right end-point of the maximal interval of existence. By
analogy with the concept of ``black hole'' solutions, that is, singular
solutions defined on 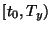 and satisfying
and satisfying
introduced by the present authors in [3] (see also [4], [7] and [8]), positive
solutions of (A) satisfying (1) as 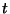 approaches the maximal existence
time
approaches the maximal existence
time 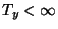 are called white hole (singular) solutions.
An example of a nonlinear equation of the form (A) (with
are called white hole (singular) solutions.
An example of a nonlinear equation of the form (A) (with 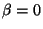 ) which
possesses singular solutions of this new type is
) which
possesses singular solutions of this new type is
where 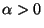 . Indeed, for any given
. Indeed, for any given  and
and 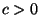 , the function
, the function
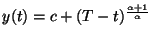 defined and positive on
defined and positive on 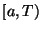 is a decreasing solution of (3) with a singularity of white hole type at
is a decreasing solution of (3) with a singularity of white hole type at 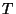 .
.
Similarly, for any 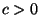 , the function
, the function
 provides an example of a `local' increasing white
hole solution of (3) which is defined and positive in some sufficiently
small left neighborhood of the maximal existence time
provides an example of a `local' increasing white
hole solution of (3) which is defined and positive in some sufficiently
small left neighborhood of the maximal existence time 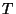 .
.
Another simple example of an equation of the form (A) having white hole
singular solutions is the following ``almost linear'' equation
As easily seen, for any real 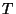 and any
and any 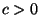 , the function
, the function
 defined and positive on
defined and positive on
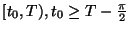 ,
is an increasing singular solution of (4) which is of the white hole type.
,
is an increasing singular solution of (4) which is of the white hole type.
While the existence and asymptotic theory for quasilinear second-order
differential equations of the form
and for singular equations
where 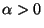 and
and 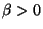 are constants and
are constants and 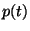 and
and
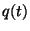 are positive continuous functions on
are positive continuous functions on  , is well
developed (see, for example, the papers [1], [5-6] and [9-11] ),
according to our knowledge there are no papers concerning the existence
of singular and proper solutions for the nonlinear equation (A)
(with
, is well
developed (see, for example, the papers [1], [5-6] and [9-11] ),
according to our knowledge there are no papers concerning the existence
of singular and proper solutions for the nonlinear equation (A)
(with 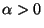 ) in our setting. This observation was one of the
motivations for the present paper.
The plan of this paper is as follows. In Section 2 we first show that,
regardless of positivity or negativity of
) in our setting. This observation was one of the
motivations for the present paper.
The plan of this paper is as follows. In Section 2 we first show that,
regardless of positivity or negativity of  , Eq. (A) always has
singular solutions of white hole type iff
, Eq. (A) always has
singular solutions of white hole type iff 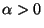 . Our procedure for
establishing the existence of such solutions for (A) is based on the
solution of appropriate nonlinear integral equation via the Schauder fixed
point theorem. Secondly, we investigate the existence of another type of
singular solutions of (A) named ``extinct solutions". More specifically, it
is shown that if either
. Our procedure for
establishing the existence of such solutions for (A) is based on the
solution of appropriate nonlinear integral equation via the Schauder fixed
point theorem. Secondly, we investigate the existence of another type of
singular solutions of (A) named ``extinct solutions". More specifically, it
is shown that if either
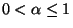 and
and
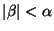 or
or
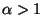 and
and
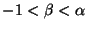 , then Eq. (A) possesses a singular
solution which extincts (together with its first derivative) at an arbitrarily
prescribed extinction point
, then Eq. (A) possesses a singular
solution which extincts (together with its first derivative) at an arbitrarily
prescribed extinction point  .
In Sections 3-5 our consideration is focused on the set of proper
solutions of (A), i.e., solutions which exist on some interval
.
In Sections 3-5 our consideration is focused on the set of proper
solutions of (A), i.e., solutions which exist on some interval
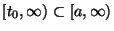 and are not identically zero in any neighborhood of
infinity. Although the equation (A) has a relativelly simple form,
the totality of proper solutions of (A) has surprisingly rich structure.
This is demonstrated in Section 3 where the set of all possible proper
solutions is classified into eight different types according to their
asymptotic behavior as
and are not identically zero in any neighborhood of
infinity. Although the equation (A) has a relativelly simple form,
the totality of proper solutions of (A) has surprisingly rich structure.
This is demonstrated in Section 3 where the set of all possible proper
solutions is classified into eight different types according to their
asymptotic behavior as 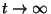 .
In Section 4 we establish conditions guaranteeing the existence of
increasing proper solutions of each of the types (IV)-(VI) appearing in
the general classification scheme given in Section 3. We prove
in particular that if
.
In Section 4 we establish conditions guaranteeing the existence of
increasing proper solutions of each of the types (IV)-(VI) appearing in
the general classification scheme given in Section 3. We prove
in particular that if
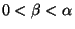 , then for any given
, then for any given 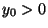 ,
Eq. (A) has a `global' solution
,
Eq. (A) has a `global' solution 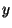 (i.e., a proper solution existing on
the whole interval
(i.e., a proper solution existing on
the whole interval  ) satisfying
) satisfying 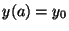 and growing to
infinity as fast as a constant multiple of
and growing to
infinity as fast as a constant multiple of 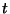 as
as 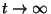 if and only
if the function
if and only
if the function 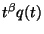 is integrable on
is integrable on  . The next
theorem in Section 4 presents sufficient conditions under which Eq. (A)
possesses an increasing proper solution which grows at infinity like a positive
constant multiple of
. The next
theorem in Section 4 presents sufficient conditions under which Eq. (A)
possesses an increasing proper solution which grows at infinity like a positive
constant multiple of
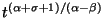 for some
for some
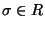 with
with
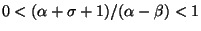 .
As regards increasing proper solutions of (A) which remain bounded as
.
As regards increasing proper solutions of (A) which remain bounded as
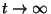 , the (`local') existence of such solutions satisfying
, the (`local') existence of such solutions satisfying
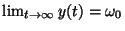 for arbitrarily prescribed terminal
value
for arbitrarily prescribed terminal
value 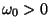 is characterized by the integral condition (38) below.
Finally, in Section 5, the existence of decreasing proper solutions of (A)
is discussed. First, it is shown that the necessary and sufficient condition
for the existence of a decreasing proper solution of (A) which remains
positive as long as it exists and tends to a given positive constant
is characterized by the integral condition (38) below.
Finally, in Section 5, the existence of decreasing proper solutions of (A)
is discussed. First, it is shown that the necessary and sufficient condition
for the existence of a decreasing proper solution of (A) which remains
positive as long as it exists and tends to a given positive constant
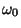 as
as 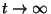 is the same as the condition characterizing
the existence of bounded increasing proper solutions for (A). Next, we
establish conditions guaranteeing the existence of positive proper solutions
which decay to zero at infinity like a positive constant multiple of the
function
is the same as the condition characterizing
the existence of bounded increasing proper solutions for (A). Next, we
establish conditions guaranteeing the existence of positive proper solutions
which decay to zero at infinity like a positive constant multiple of the
function
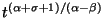 for some
for some 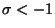 where
where
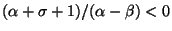 . We end Section 5 with
the existence result characterizing the situation in which Eq. (A)
(with
. We end Section 5 with
the existence result characterizing the situation in which Eq. (A)
(with
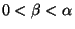 ) possesses an eventually negative decreasing
proper solution emanating from a given point
) possesses an eventually negative decreasing
proper solution emanating from a given point
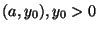 , with
specific asymptotic behavior as
, with
specific asymptotic behavior as 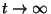 .
.



Next: Bibliography
Up: On White Hole Solutions
Previous: On White Hole Solutions
Nobuki Takayama
2003-01-30
![]() , the function
, the function
![]() provides an example of a `local' increasing white
hole solution of (3) which is defined and positive in some sufficiently
small left neighborhood of the maximal existence time
provides an example of a `local' increasing white
hole solution of (3) which is defined and positive in some sufficiently
small left neighborhood of the maximal existence time ![]() .
.