


Next: Bibliography
Up: EXISTENCE OF POSITIVE SOLUTIONS
Previous: EXISTENCE OF POSITIVE SOLUTIONS
This paper presents three new existence results for semipositone
Fredholm integral equations of the form
where 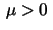 is a constant. Existence in both
is a constant. Existence in both ![$\,C[0,1]\,$](img9.png) and
and
![$\,L^p[0,1]\,$](img10.png) will be discussed.
Throughout this paper
will be discussed.
Throughout this paper 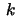 is nonnegative
but our nonlinearity
is nonnegative
but our nonlinearity 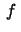 may take negative values.
Problems of this type are referred to as semipositone problems in the
literature and they arise naturally in chemical reactor theory [4]. The
constant
may take negative values.
Problems of this type are referred to as semipositone problems in the
literature and they arise naturally in chemical reactor theory [4]. The
constant 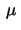 is called the Thiele modulus and of physical interest is
the existence of positive solutions to
is called the Thiele modulus and of physical interest is
the existence of positive solutions to  when
when 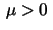 is small. The literature on positive solutions to Fredholm integral equations
(see [3]-[8]] and the references therein) is almost totally devoted to
is small. The literature on positive solutions to Fredholm integral equations
(see [3]-[8]] and the references therein) is almost totally devoted to  when
when 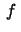 takes nonnegative values (i.e. positone problems). Only a few
results (see [1, Chapter 4]) are available for the semipositone problem.
takes nonnegative values (i.e. positone problems). Only a few
results (see [1, Chapter 4]) are available for the semipositone problem.
Existence in this paper will be established using
Krasnoselskii's fixed point theorem in a
cone, which we state here for the convenience of the reader.
Theorem 1.1. Let
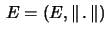 be a Banach space and let
be a Banach space and let
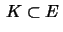 be a cone in
be a cone in 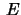 . Assume
. Assume 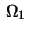 and
and 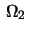 are open subsets of
are open subsets of  with
with
 and
and
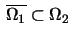 and let
and let
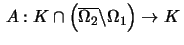 be
continuous and completely continuous. In addition suppose either
be
continuous and completely continuous. In addition suppose either
or
hold. Then 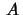 has a fixed point in
has a fixed point in
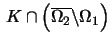 .
.



Next: Bibliography
Up: EXISTENCE OF POSITIVE SOLUTIONS
Previous: EXISTENCE OF POSITIVE SOLUTIONS
Nobuki Takayama
2002-09-18
![]() be a Banach space and let
be a Banach space and let
![]() be a cone in
be a cone in ![]() . Assume
. Assume ![]() and
and ![]() are open subsets of
are open subsets of ![]() with
with
![]() and
and
![]() and let
and let
![]() be
continuous and completely continuous. In addition suppose either
be
continuous and completely continuous. In addition suppose either