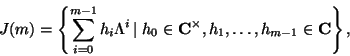
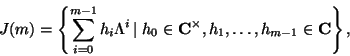

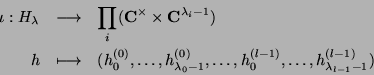
Let
![]() be an
be an ![]() -tuple of complex numbers satisfying
-tuple of complex numbers satisfying
![]() We define the character
We define the character
![]() of the universal covering group
of the universal covering group
![]() of
of ![]() by
by
![]() , where
, where
![\begin{displaymath}\chi(h^{(i)};\alpha ^{(i)})=h_0^{\alpha _0^{(i)}}\exp\left[\s...
...ts, \frac {h^{(i)}_{\lambda _i-1}}{ h\sb{0}^{(i)}}\big)\right] \end{displaymath}](img21.png)
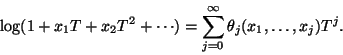
Recall that the hypergeometric function
![]() of type
of type ![]() (see
[7]) is a function defined by
(see
[7]) is a function defined by
The set ![]() admits an action of the group
admits an action of the group
![]()
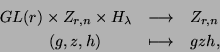
The hypergeometric functions ![]() on
on ![]() and
and ![]() for various partitions
for various partitions ![]() of 4 and 5 were investigated in the papers [7],
[9] and [8].
It is known that the functions
of 4 and 5 were investigated in the papers [7],
[9] and [8].
It is known that the functions ![]() are generalizations of Gauss', Kummer's, Bessel's, Hermite's, Airy's functions and the classical hypergeometric functions of two variables, i.e.,
are generalizations of Gauss', Kummer's, Bessel's, Hermite's, Airy's functions and the classical hypergeometric functions of two variables, i.e.,
![]() in Horn's list ([3]). In this paper, we study the hypergeometric functions of type
in Horn's list ([3]). In this paper, we study the hypergeometric functions of type ![]() in two variables on the strata of the set
in two variables on the strata of the set
![]() of
of ![]() complex matrices.We establish a classification of the functions in terms of the orbital decomposition of the set of strata and give some transformation formulae between some systems of differential equations satisfied by the functions
complex matrices.We establish a classification of the functions in terms of the orbital decomposition of the set of strata and give some transformation formulae between some systems of differential equations satisfied by the functions
![]()
In Section 1 , we introduce a group
![]() which is analogous to the (classical) Weyl group and discuss its properties in detail. In Section 2, we consider the action of
which is analogous to the (classical) Weyl group and discuss its properties in detail. In Section 2, we consider the action of
![]() on the set
on the set
![]() of strata and obtain the orbital decomposition of
of strata and obtain the orbital decomposition of
![]() . In Section 3, we obtain suitable normal forms of the matrices in the strata relative to the action of
. In Section 3, we obtain suitable normal forms of the matrices in the strata relative to the action of
![]() . Then we can reduce the hypergeometric function
. Then we can reduce the hypergeometric function ![]() into a function of two variables. In Section 4, we give relations between the classical special functions of hypergeometric type, i.e., Appell's
into a function of two variables. In Section 4, we give relations between the classical special functions of hypergeometric type, i.e., Appell's ![]() ,
, ![]() ,
, ![]() and their confluence in Horn's list, and the hypergeometric functions of type
and their confluence in Horn's list, and the hypergeometric functions of type ![]() in two variables. In the last section, some
transformation formulae for the systems of diffenentical equations are systematically
deduced from the symmetries
in two variables. In the last section, some
transformation formulae for the systems of diffenentical equations are systematically
deduced from the symmetries
![]() -
-
![]() for the functions
for the functions ![]() .
.
The author expresses his deep gratitude to Prof. Kazuo Okamoto, Prof. Hironobu Kimura and Prof. Katsunori Iwasaki for their valuable suggestions and kind help during the preparation of this paper.