This investigation is a sequel of our previous work [3]
where we studied the existence, uniqueness, nonuniqueness and radial property of viscosity solutions of the Dirichlet problem for the semilinear degenerate elliptic equation
The main purpose of the present paper is to prove existence of viscosity solutions, and to give a sufficient condition assuring the uniqueness and the radial symmetry of viscosity solutions of (DP). In what follows we consider the problem (DP) in case ![]() , since we can treat it in case
, since we can treat it in case ![]() by the same arguments.
by the same arguments.
Throughout this paper we make the following assumptions:
(H1)
![]() is strictly increasing in
is strictly increasing in ![]() for each fixed
for each fixed ![]() .
.
(H2) There exists an implicit function ![]() of
of ![]() satisfying
satisfying

It is clear that ![]() is continuous on
is continuous on ![]() by (H1) and (H2).
by (H1) and (H2).
We state our existence theorem.
In order to establish the uniqueness of viscosity solutions for (DP) we introduce additional assumptions and a notion of standard viscosity solution.
(H3)
![]() here
here ![]() is the function defined in (H2).
is the function defined in (H2).
(H4) The function ![]() satisfies the condition : if
satisfies the condition : if ![]() then
then
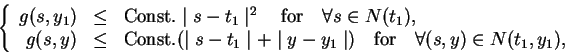
(H5) For ![]() and
and ![]() , we impose the following structure condition : if
, we impose the following structure condition : if
![]() ,
, ![]() and
and
![]() , then
, then
Example Let
![]() . Define
. Define
![]() by
by
(i) for every ![]() ,
,
(i-1) ![]() for all
for all
![]() and all
and all
![]() ,
,
(i-2)
![]() for all
for all
![]() ,
,
(i-3)
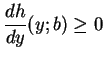 for all
for all
![]() ,
,
(i-4)
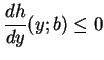 for all
for all
![]() ;
;
(ii) for
![]() for all
for all ![]() , i.e.,
, i.e.,
![]() for
for
![]() .
.
Here, for every
![]() . Suppose
. Suppose
![]() , and that
, and that
![]() is a given function satisfying
is a given function satisfying
![]() for every
for every ![]() such that
such that ![]() . Then
. Then ![]() and
and ![]() satisfy the assumptions (H1)-(H5).
satisfy the assumptions (H1)-(H5).
Definition.
A function ![]() is called a standard viscosity solution of (DP) if
is called a standard viscosity solution of (DP) if ![]() is a viscosity solution and
is a viscosity solution and
![]() for all
for all
![]() satisfying
satisfying ![]() .
.
By making use of a notion of standard viscosity solutions, we shall prove the uniqueness for (DP) :
The authors would like to express their hearty gratitude to the referee for kind and helpful advice.